1 坐标系与位姿变换

1.1 目标：

理解机器人运动的空间表示，掌握齐次变换矩阵的使用。

1.2 内容：

1.2.1 笛卡尔坐标系：

“机器人的空间视角”

这是人类最直观的理解方式。它基于我们熟悉的直角坐标系，描述的是机器人末端工具中心点 (TCP) 在空间中的位置和方向。

定义： 描述机器人末端相对于基座（Base）或世界（World）的位置和姿态。
数据表示： 通常包含 6 个值：3 个位置值 + 3 个方向值。

- 位置 (Location): $X, Y, Z$ (前后、左右、上下)。

- 姿态 (Orientation): $R x, R y, R z$ (或 $A, B, C$ / $W, P, R$ )，表示绕轴的旋转（如翻滚、俯仰、偏航）。

1.2.2 关节坐标系：

“机器人的内部视角”

这是机器人最原始的控制方式。在这个坐标系下，机器人的每一个位置都是由每个关节的旋转角度（或移动距离）来定义的。

定义： 通过直接控制机器人各个轴（电机）的旋转角度来确定机器人的姿态。
数据表示： 如果是一个六轴机器人，其坐标数据通常表示为一组角度，例如： $(J_{1}, J_{2}, J_{3}, J_{4}, J_{5}, J_{6})$ 。

- 例如： $J_{1} = 30^{\circ}, J_{2} = - 45^{\circ}, \dots$

1.2.3 齐次矩阵（4×4）表示位姿

齐次变换矩阵（Homogeneous Transformation Matrix） 是描述物体在空间中 **“位置”和“姿态”**最重要的数学工具。

T = [\begin{matrix} R_{3 \times 3} & P_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{matrix}] = [\begin{matrix} r_{11} & r_{12} & r_{13} & p_{x} \\ r_{21} & r_{22} & r_{23} & p_{y} \\ r_{31} & r_{32} & r_{33} & p_{z} \\ 0 & 0 & 0 & 1 \end{matrix}]

A. 左上角 $3 \times 3$ ：旋转矩阵 (Rotation)

[\begin{matrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{matrix}]

这一块描述了姿态（Orientation）。
它定义了物体的坐标轴相对于参考系是如何偏转的。
这些数字通常是由欧拉角（Rx, Ry, Rz）计算出来的余弦和正弦值。

B. 右上角 $3 \times 1$ ：位置向量 (Position / Translation)

[\begin{matrix} p_{x} \\ p_{y} \\ p_{z} \end{matrix}]

这一块描述了位置（Location）。
它非常直观，就是坐标系原点相对于参考系的 $X, Y, Z$ 距离。

C. 最后一行：比例与透视 (Scale & Perspective)

[\begin{matrix} 0 & 0 & 0 & 1 \end{matrix}]

在工业机器人这种“刚体运动”中，物体不会变大变小，也不会发生透视变形。
所以这一行永远是固定的 $[0, 0, 0, 1]$ 。它存在的意义主要是为了凑成 $4 \times 4$ 的方阵，以便进行矩阵运算。

1.2.4 平移、旋转（欧拉角、四元数）

平移： 主要就是坐标原点的运动

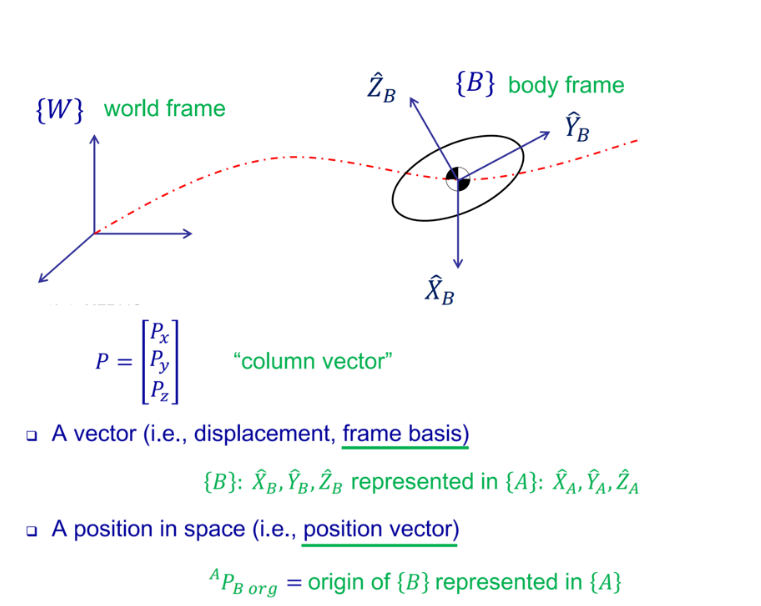
旋转：

右乘： $T_{n e w} = T_{o l d} \times R$

物理意义：绕“自身”（当前）的坐标轴旋转 (Intrinsic Rotation)

这是机器人学中最常用的逻辑。

想象你就是那个坐标系（或者机器人末端）：

- 当你已经在空间中处于某个姿态 $T_{o l d}$ 了。

- 指令是：“绕你自己的 Z 轴（你的头顶方向）转 90 度”。

- 这时候，旋转矩阵 $R$ 必须乘在右边。

应用场景：

- 工具操作： 机器人末端已经伸出去了，现在要让电钻转动，或者让夹具旋转一下。这是相对于工具本身的旋转。

- 连杆推导： 在推导机械臂正运动学（如 DH 参数）时，我们通常是一个关节接一个关节地往后推，这本质上是一连串的右乘（相对于上一关节移动/旋转）。

—

左乘： $T_{n e w} = R \times T_{o l d}$

物理意义：绕“固定”（世界/基座）的坐标轴旋转 (Extrinsic Rotation)

想象你在玩操纵木偶：

- 木偶在舞台的某个位置 $T_{o l d}$ 。

- 指令是：“绕**舞台中心（世界原点）**的 Z 轴转 90 度”。

- 这时候，旋转矩阵 $R$ 必须乘在左边。

- 结果： 整个物体会绕着世界原点画圆弧，发生巨大的位置位移。

应用场景：

- 基座调整： 如果你把整个机器人搬起来，把底座旋转了 30 度。那么机器人末端相对于世界的位置，就是左乘了这个 30 度的变换。

- 坐标系校正： 比如传感器安装歪了，需要在最外层套一个修正矩阵。

欧拉角：

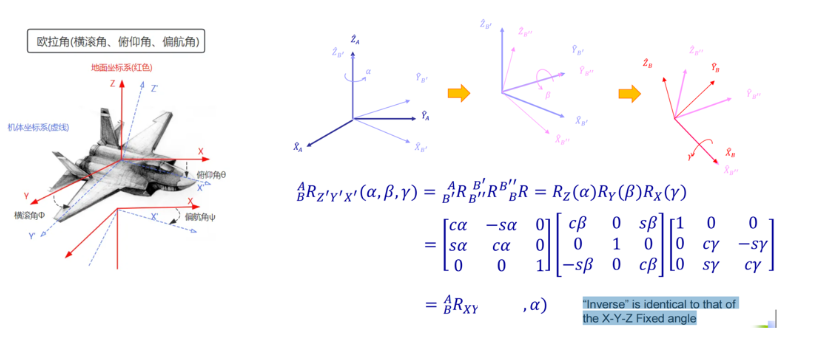
四元数：

比欧拉角多一个自由度。优点是可以避免万向节死锁。

1.2.5 坐标系之间的转换与链式计算

坐标计算可用链式计算进行转换

链式计算举例：

World (W): 世界大地（固定不动）。
Base (B): 机器人底座（安装在地面上，可能有个偏移）。
Flange (F): 机器人末端法兰盘（随关节转动）。
Tool (T): 安装在法兰上的夹具（TCP）。

问题： 我控制了关节运动，夹具尖端 (Tool) 在世界 (World) 的哪里？

链式计算公式：

^{W} T_{T} =^{W} T_{B} \times^{B} T_{F} \times^{F} T_{T}

$^{W} T_{B}$ (Base Frame): 机械臂装在哪里？（通常是固定的安装误差矩阵）。
$^{B} T_{F}$ (Kinematics): 这一项是动态变化的。它是通过 6 个关节角度 $(J_{1} . . . J_{6})$ 算出来的（正运动学）。
$^{F} T_{T}$ (Tool Frame): 夹具有多长？（这是你标定出来的，通常固定不变）。

只要把这三个 $4 \times 4$ 矩阵按顺序乘起来，得到的结果 $^{W} T_{T}$ 的最后一列 $(x, y, z)$ 就是夹具尖端的世界坐标。

机器人基础——坐标系与位姿变换(1).docx

1.3 问题：

1.3.1 为什么需要用一个整体的“齐次矩阵”来表示位姿，而不是分开用旋转和位移？

齐次矩阵包含了旋转与位移，同时使用齐次矩阵可以更方便的进行坐标变换。

例如需要进行位移或者旋转，只需要将齐次矩阵乘上对应的变换矩阵即可实现变换，

引入矩阵乘法，实现相对坐标到实际三位坐标的转换，这有利于运动学正逆解的求解

1.3.2 如果一个点在 A 坐标系下有坐标，我们如何把它转换到 B 坐标系？

求解出A到B的坐标系变换矩阵，求解方法为：

然后A坐标系的坐标乘上这个变换矩阵

1.3.3 多个关节坐标系之间的变换，最后是如何得到末端相对基座的位姿的？

通过矩阵链式法则 (Chain Rule) 计算。既然每个关节相对于上一级关节的变换矩阵是已知的（由 DH 参数或关节角度决定），我们只需将这些局部变换矩阵按顺序连乘。公式为： $^{Base} T_{End} =^{Base} T_{1} \times^{1} T_{2} \times \dots \times^{n - 1} T_{End}$ 。最终得到的矩阵，其平移部分和旋转部分即代表末端相对于基座的位姿。

2 轨迹规划

2.1 目标：

理解机器人从起点到终点的运动方式和路径生成。

2.2 内容：

2.2.1 插值方法（直线插值、多项式插值）

插值就是将路径点变得更加密集，如何选择添加原本没有的路径点，需要定义新点坐标与老坐标的关系式。

直线插值 (Linear Interpolation with Parabolic Blends, LSPB)
这是最简单、最直观的插值方法，也称为“线性插值”。

基本原理

它的核心思想是：两点确定一条直线。

如果你想知道两个已知点 $(x_{0}, y_{0})$ 和 $(x_{1}, y_{1})$ 之间某个 $x$ 对应的 $y$ 值，我们就假设这两点之间是用一把直尺连起来的，直接算这条直线上的点。

数学公式

假设要在 $x_{0}$ 和 $x_{1}$ 之间插值求 $x$ 处的 $y$ ：

y = y_{0} + (x - x_{0}) \frac{y_{1} - y_{0}}{x_{1} - x_{0}}

这个公式的直观理解是：

$y_{0}$ ：起始高度。
$\frac{y_{1} - y_{0}}{x_{1} - x_{0}}$ ：斜率（变化率）。
$(x - x_{0})$ ：你从起点走了多远。

特点

优点：计算非常快，逻辑简单，永远不会出现极端的数值波动（稳定）。
缺点：不光滑。在数据点连接处会有尖角（导数不连续），不够精确。它只能模拟线性变化，无法模拟弯曲的趋势。

2. 多项式插值 (Polynomial Interpolation)
当你觉得直线太生硬，想要一条平滑的曲线穿过所有数据点时，就会用到多项式插值。

基本原理

它的核心思想是：用一个高次多项式函数来穿过所有已知的点。

数学上有一个定理：给定 $n + 1$ 个不同的点，恰好存在一个次数不超过 $n$ 的多项式通过这些点。

2个点 $\to$ 一次多项式（直线）
3个点 $\to$ 二次多项式（抛物线）
$n + 1$ 个点 $\to$ $n$ 次多项式

常见的计算方法包括拉格朗日插值法 (Lagrange Interpolation) 和 牛顿插值法 (Newton Interpolation)。

数学形式

寻找一个函数 $P (x)$ ：

P (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{1} x + a_{0}

使得对于每一个已知点 $x_{i}$ ，都有 $P (x_{i}) = y_{i}$ 。

特点

优点：生成的曲线非常光滑（处处可导），对于本身就是平滑变化的物理规律模拟得更好。
缺点：
1. 计算复杂：点越多，多项式的次数越高，计算量越大。
2. 龙格现象 (Runge’s Phenomenon)：这是一个致命弱点。当插值的点非常多（多项式次数很高）时，在区间的边缘，曲线会发生剧烈的震荡（上下乱窜），导致插值结果完全不可信。

2.2.2 笛卡尔空间轨迹 vs 关节空间轨迹

2.2.2.1 笛卡尔空间

也常被称为任务空间 (Task Space) 或 操作空间 (Operational Space)。

定义

笛卡尔空间是用机器人末端执行器（手/夹爪）在空间中的坐标和姿态来描述状态。

它通常由位置 ( $x, y, z$ ) 和姿态 (如欧拉角 Roll, Pitch, Yaw) 组成。

变量表示：通常用 $x$ 或 $P$ 表示。
- 例如： $x = [100 m m, 200 m m, 500 m m, 0^{\circ}, 90^{\circ}, 0^{\circ}]$
- 这意味着：手在坐标 (100, 200, 500) 的位置，并且手掌垂直向下（假设 Pitch 90度是向下）。

2.2.2.2 关节空间 (Joint Space)

定义

关节空间是用机器人每个关节的角度或位移来描述机器人的状态。

如果一个机器人有 6 个电机（关节），那么关节空间就是一个由这 6 个电机的角度组成的向量。

变量表示：通常用 $θ$ (theta) 或 $q$ 表示。
- 例如： $q = [30^{\circ}, - 45^{\circ}, 90^{\circ}, 10^{\circ}, 0^{\circ}, 60^{\circ}]$
- 这意味着：第一个关节转30度，第二个转-45度，以此类推。

直观理解

想象你闭着眼睛伸手。你虽然看不见手在哪里，但你的大脑清楚地知道你的“肩膀转了多少度”、“手肘弯了多少度”。

对于机器人来说：这是最自然的描述方式，因为机器人控制器直接控制的是电机的转动。

特点

控制简单：直接给电机发送指令即可。
路径非直观：如果你在关节空间让所有关节均匀转动（线性插值），机器人的手（末端）在空中画出的轨迹通常是一条复杂的弧线，而不是直线。

直观理解

这就好比你告诉别人：“把桌子上的杯子从坐标 A 拿到坐标 B”。你不关心对方的手肘怎么弯曲，你只关心杯子（末端）在空间里的位置变化。

特点

直观：符合人类的直觉，方便规划任务（例如：画一条直线、画一个圆）。
控制复杂：电机听不懂“去坐标 (x,y,z)”，控制器必须经过复杂的数学计算（逆运动学），把坐标转换成关节角度才能驱动电机。

2.2.2.3 对比

特性	关节空间 (Joint Space)	笛卡尔空间 (Cartesian Space)
描述对象	机器人的关节/电机	机器人的手/末端
数据形式	一组角度 ( $θ_{1}, θ_{2} . . .$ )	坐标+姿态 ( $x, y, z, R x, R y, R z$ )
规划直线	容易规划，但末端轨迹是弧线	规划容易，末端轨迹是直线
计算量	小（不需要复杂变换）	大（需要计算逆运动学）
奇点问题	无（除非机械限位）	有（可能会遇到无法到达的姿态）
谁更喜欢	机器人底层的电机控制器	设定任务的操作员/程序员

两者之间的桥梁：运动学

机器人在工作时，这两个空间的数据需要不断互相转换：

正运动学 (Forward Kinematics, FK)：
- 已知：关节角度（关节空间）。
- 求解：手在哪里（笛卡尔空间）。
- 难度：很简单，有唯一解。
- 场景：机器人显示当前的坐标读数。
逆运动学 (Inverse Kinematics, IK)：
- 已知：手要去哪里（笛卡尔空间）。
- 求解：关节要转多少度（关节空间）。
- 难度：很难，可能有多个解（比如手摸后脑勺，手肘可以朝上也可以朝下），也可能无解（目标太远够不着）。
- 场景：你命令机器人“去抓那个苹果”。

总结

如果你想让机器人走得快且稳，通常在关节空间规划运动（点到点运动，PTP）。
如果你想让机器人画直线、涂胶水或焊接，必须在笛卡尔空间规划运动（直线插值运动，LIN）。

2.2.3 时间参数化与速度/加速度约束

仅仅画出一条路径（Path）是不够的，我们还需要决定机器人“走多快”，这就是时间参数化 (Time Parameterization)。

2.2.3.1 时间参数化

在机器人学中，我们通常把“路径”和“轨迹”区分得很清楚：

路径 (Path)：只是一条空间中的几何曲线。它只有位置信息，没有时间概念。
- 例子：地图上从北京到上海的一条红线。
轨迹 (Trajectory)：是路径 + 时间信息。它规定了机器人在每一个时间点 $t$ 应该在路径的哪个位置。
- 例子：高铁时刻表（8:00在北京，10:00在济南，12:30到上海）。

时间参数化就是把“路径”变成“轨迹”的过程。
数学原理

假设我们已经用插值法算出了一条路径 $P (s)$ ，其中 $s$ 是一个归一化的参数（ $s = 0$ 是起点， $s = 1$ 是终点）。

时间参数化就是寻找一个函数 $s (t)$ ，把时间 $t$ 映射到路径进度 $s$ 上。

如果 $s (t)$ 是线性的（ $s = k \cdot t$ ），机器人就匀速运动。
如果 $s (t)$ 是S形的，机器人就会先加速、再匀速、最后减速。

2.2.3.2 速度/加速度约束

既然我们可以随意定义 $s (t)$ ，那能不能让机器人 0.01秒就从起点飞到终点？

当然不行。这就是约束发挥作用的地方。

机器人的物理能力是有限的，我们必须在规划 $s (t)$ 时遵守以下限制：

A. 速度约束 (Velocity Constraints)

定义：机器人的关节或末端移动的最大快慢。
原因：
- 电机有最高转速限制（转太快会烧或者失控）。
- 任务要求（比如涂胶水如果走太快，胶水就断了）。
数学表现： $| \frac{d s}{d t} | \leq v_{m a x}$

B. 加速度约束 (Acceleration Constraints)

定义：机器人速度变化的快慢。
原因：
- 力矩限制：牛顿第二定律 $F = m a$ 。加速度越大，需要的力（电机扭矩）就越大。电机扭矩是有限的。
- 机械磨损：急起急停（加速度过大）会产生巨大的冲击力，导致减速机磨损、皮带断裂或机身抖动。
数学表现： $| \frac{d^{2} s}{d t^{2}} | \leq a_{m a x}$

在实际的轨迹规划算法（如梯形速度规划）中，流程是这样的：

几何规划：先用插值法画出路径（比如一条直线）。
施加约束：查阅机器人的手册，比如最大速度 $v_{m a x} = 1 m / s$ ，最大加速度 $a_{m a x} = 2 m / s^{2}$ 。
计算时间参数化 $s (t)$ ：
- 为了效率，我们通常希望机器人尽快到达终点。
- 算法会计算：用最大的加速度 $a_{m a x}$ 加速，直到达到最大速度 $v_{m a x}$ ，保持匀速，快到终点时再用最大加速度（负值）减速。
- 这就是著名的梯形速度曲线 (Trapezoidal Velocity Profile)。

2.2.4 基本规划算法（RRT、PRM 简介）

2.2.4.1 RRT (Rapidly-exploring Random Tree)

从专业的角度来看，RRT 是一种用于在非凸高维空间中快速搜索可行路径的数据结构和算法策略。

数学本质：空间填充曲线（Space-filling Curve）的随机化变体

RRT 的核心理论属性是Voronoi 偏差（Voronoi Bias）。在数学上，树上的每一个节点都支配着空间中的一个 Voronoi 区域。处于搜索树“前沿”的节点拥有最大的 Voronoi 区域，因此随机采样点落入这些区域的概率最大。这使得 RRT 能够自适应地引导搜索树向未探测的开阔区域（Unexplored Region）快速扩展，而不是在已探索区域内停滞。
处理动力学约束（Kinodynamic Planning）的能力

与其他几何规划算法不同，RRT 的扩展过程本质上是对系统状态方程 $\dot{x} = f (x, u)$ 的正向积分。这意味着它不需要解两点边值问题（BVP），天然适合处理带有非完整约束（Non-holonomic Constraints）或微分约束的系统（例如：车辆不能横移、机械臂的速度加速度限制）。
拓扑特征：树（Tree）

它构建的是一个**单连通（Simply Connected）**的拓扑结构。从根节点（起点）到树上任意节点只有唯一的路径，不包含环路。

2.2.4.2 PRM (Probabilistic Roadmap)

从专业的角度来看，PRM 是一种用离散图论模型近似连续拓扑空间的映射方法。

数学本质：连通性图谱（Connectivity Graph）

PRM 的目标不是直接求解路径，而是捕捉自由空间（ $C_{f r e e}$ ）的拓扑结构。它通过随机采样将连续的 $C_{f r e e}$ 离散化为一个无向图（Roadmap）。如果两个采样点之间存在无碰撞的直线路径（或其他简单路径），则认为它们在拓扑上是连通的。
窄通道问题（Narrow Passage Problem）

PRM 的一个主要理论瓶颈在于对“体积微小但对连通性至关重要的区域”的采样效率低。在概率论上，均匀采样落入狭窄通道的概率与其体积成正比，导致在这些关键区域难以形成连通的边，从而造成图谱的断裂。
拓扑特征：图（Graph）

它构建的是一个 多连通（Multiply Connected） 的网络结构，包含环路。这为规划器提供了多条可选的同伦路径（Homotopic Paths）。

特性	RRT (随机树)	PRM (路图)
结构形态	树 (Tree)：有根，无环路	图 (Graph)：网状，有环路
使用场景	单次任务：我只走这一回，走完就撤	多次任务：我以后天天要在这走
环境要求	适合动态环境，或者不知道全图时	适合静态环境，必须预先知道全图
计算分布	每次找路都要花中等时间	第一次极慢（建图），后面极快（查表）
高维表现	非常好（适合 7轴、12轴机械臂）	也不错，但连接点耗时更多
典型比喻	闪电探路	地铁线路图
什么时候用哪个？

用 RRT：如果你是一个无人机在未知的森林里飞，你需要一边飞一边探测，环境随时在变，或者你只是偶尔过一次，不想费劲建全图。
用 PRM：如果你是一个仓库里的搬运机器人，仓库里的货架（障碍物）永远不动，你需要一天跑几百趟不同的路线。

_通常在机械臂规划中，RRT（及其改进版 RRT-Connect, RRT）用得更多，因为机械臂的状态空间太大了，建一张完美的 PRM 图往往太耗内存。_*
具身智能基础——机器人轨迹规划.docx

2.3 问题：

2.3.1 为什么在关节空间直线运动和在笛卡尔空间直线运动会产生不同的轨迹？

这是一个非常经典且深刻的问题，它触及了机器人学的核心数学本质：非线性映射 (Non-linear Mapping)。

根本原因在于：关节空间（角度）与笛卡尔空间（位置）之间的映射关系通常是包含三角函数（sin, cos）的非线性关系，而不是简单的比例关系。

下面为您详细拆解其中的数学原理和物理表现。

核心数学原因：非线性运动学

机器人的正运动学（Forward Kinematics）方程描述了关节角度 $q$ 如何决定末端位置 $x$ 。对于旋转关节的机械臂，这个方程通常长这样：

x = l_{1} \cos (q_{1}) + l_{2} \cos (q_{1} + q_{2})

y = l_{1} \sin (q_{1}) + l_{2} \sin (q_{1} + q_{2})

请注意其中的 $\cos$ 和 $\sin$ 。

情况 A：在关节空间做直线运动 (Joint Interpolation)

这意味着让角度 $q$ 随时间 $t$ 线性变化（匀速转动）：

q (t) = k \cdot t

如果你把这个线性的 $q (t)$ 代入上面的公式，你会发现末端位置 $x (t)$ 变成了：

x (t) = l_{1} \cos (k \cdot t) + \dots

结论： $x$ 随时间的变化是余弦波形，而不是线性的。在几何上，这意味着末端画出的是圆弧或复杂的曲线，而不是直线。

情况 B：在笛卡尔空间做直线运动 (Cartesian Interpolation)

这意味着强行规定末端位置 $x, y$ 随时间 $t$ 线性变化：

x (t) = v_{x} \cdot t

为了实现这一点，控制器必须反推关节角度 $q (t)$ 应该怎么变（逆运动学）：

q (t) = \arccos (\frac{x (t) - \dots}{\dots})

结论：为了让末端走直线，关节必须以一种非线性的、忽快忽慢的节奏去转动（因为反余弦函数 $\arccos$ 是非线性的），以此来抵消旋转带来的弧度。
假设你要在面前的白板上画一条水平横线。

关节空间直线插值：
- 如果你只让肩膀关节匀速转动，手肘不动，你的手会在空中画出一个以肩膀为圆心的扇形弧线。这就是关节空间的“直线”（在角度图上是直线，在空间中是圆弧）。
笛卡尔空间直线插值：
- 为了画出直的横线，当你肩膀转动时，你的手肘必须配合着伸缩/弯曲。
- 当手伸到最远端时，手肘要伸直；当手划过身体正前方（最近点）时，手肘要弯曲得最厉害。
- 这种“肩膀转一点，手肘就要精密计算着弯一点”的过程，就是笛卡尔空间插值。

2.3.2 轨迹规划时，为什么要限制速度和加速度？

这不仅仅是为了“平滑”，而是受限于物理定律和硬件极限。

动力学限制 (Dynamics & Torque Saturation)

请看拉格朗日动力学方程：

\tau = \mathbf{M}(q)\ddot{q} + \mathbf{C}(q, \dot{q})\dot{q} + \mathbf{G}(q)

- 限制加速度 ( $\ddot{q}$ )：由第一项 $M (q) \ddot{q}$ 可知，力矩 $τ$ 与加速度成正比。如果 $\ddot{q}$ 过大，所需的 $τ$ 会超过电机的额定峰值力矩 $τ_{p e a k}$ 。一旦超过，电机无法提供足够的力，机器人就会偏离轨道（Tracking Error）。

- 限制速度 ( $\dot{q}$ )：由第二项 $C (q, \dot{q}) \dot{q}$ 可知，科里奥利力和离心力与速度的平方成正比。速度翻倍，非线性干扰力变为 4 倍，这会极大地破坏控制系统的稳定性。

电机物理限制

- 反电动势 (Back-EMF)：直流电机的电压方程 $V = I R + K_{e} \dot{q}$ 。当 $\dot{q}$ 过高时，反电动势 $K_{e} \dot{q}$ 可能会接近电源电压，导致没有电压差来驱动电流 $I$ ，电机输出力矩骤降为 0。

机械共振 (Resonance)

- 过大的加速度突变（即加加速度 Jerk）会激发机械臂连杆的低频模态，导致末端剧烈抖动。

2.3.3 如果规定两秒钟必须完成一次动作，应该如何安排轨迹？

这通常通过多项式插值（Polynomial Interpolation）或速度曲线缩放来实现。以下是具体的实施步骤和数学逻辑：

方法一：五次多项式插值 (Quintic Polynomial) —— 最推荐

这是工业机器人和服务机器人中最常用的方法，因为它能保证在起点和终点时，速度和加速度都为 0（平滑启动，平滑停止）。

设定边界条件

假设这一动作是从位置 $q_{0}$ 移动到 $q_{f}$ ，总时间 $T = 2$ 秒。我们需要满足 6 个条件：

$t = 0$ (起点): 位置= $q_{0}$ ，速度=0，加速度=0
$t = 2$ (终点): 位置= $q_{f}$ ，速度=0，加速度=0

建立方程

我们使用一个关于时间 $t$ 的五次多项式：

q (t) = a_{0} + a_{1} t + a_{2} t^{2} + a_{3} t^{3} + a_{4} t^{4} + a_{5} t^{5}

求解系数

直接将 $T = 2$ 和边界条件代入，可以解出这 6 个系数（这是一个标准的线性方程组求解）：

$a_{0} = q_{0}$
$a_{1} = 0$
$a_{2} = 0$
$a_{3} = \frac{10 (q_{f} - q_{0})}{T^{3}} = \frac{10 Δ q}{8} = 1.25 Δ q$
$a_{4} = \frac{- 15 (q_{f} - q_{0})}{T^{4}} = \frac{- 15 Δ q}{16}$
$a_{5} = \frac{6 (q_{f} - q_{0})}{T^{5}} = \frac{6 Δ q}{32}$

生成指令

现在你有了具体的函数 $q (t)$ 。在控制周期（比如 1ms）内，不断代入 $t = 0.001, 0.002 . . . 2.0$ ，算出每一个时刻应该在的位置发送给电机即可。

方法二：梯形速度曲线倒推 (Trapezoidal Profile Scaling) —— 工程常用

如果你习惯用“加速-匀速-减速”的逻辑，可以通过时间反推速度。
逻辑分析

要在 2秒内走完距离 $L$ 。

如果全程匀速（不可能），速度 $v = L / 2$ 。
因为有加减速过程，峰值速度 (Peak Velocity) 必须大于平均速度。

设定比例

通常设定加速时间 $t_{a c c}$ 和减速时间 $t_{d e c}$ 。为了简单，常设 $t_{a c c} = t_{d e c} = τ$ 。

假设加速段占总时间的 20%（即 0.4秒），减速段占 20%。

匀速段时间 = $2.0 - 0.4 - 0.4 = 1.2$ 秒。

计算峰值速度

根据面积法（速度-时间图像的面积 = 距离）：

L = v_{p e a k} \times (T_{t o t a l} - τ)

v_{p e a k} = \frac{L}{2.0 - 0.4} = \frac{L}{1.6}

这意味着，你只需将机器人的最大速度设定为 $\frac{L}{1.6}$ ，并设定加速度 $a = v_{p e a k} / 0.4$ ，就能精确在 2秒跑完。

关键步骤：可行性校验 (Feasibility Check)

这是最重要的一步。你规定了 2秒，但机器人不一定做得到。

在生成轨迹后，你必须立刻检查：

最大速度检查：计算出的 $v_{p e a k}$ 是否超过了电机铭牌上的最大转速？
最大加速度检查：五次多项式的最大加速度发生在 $t$ 的中间段附近，计算它是否超过了电机的最大扭矩限制？

如果没超过：恭喜，轨迹有效。
如果超过了：物理上不可能完成。你必须报错：“Target time 2.0s is unreachable (Requires velocity X > Limit)”。

3 机器人运动学

3.1 目标：

建立关节运动与末端位姿的数学关系，理解 IK/FK。

3.2 内容：

3.2.1 FK（正运动学）：

已知关节角 → 计算末端位姿

3.2.2 IK（逆运动学）：

已知末端位姿 → 计算关节角

3.2.3 奇异性与冗余度问题

想要快速了解什么是IK FK的同学可以看这个7分钟的短片, 可以对此建立一个粗略的认知：BiliBili 较为简单的过一遍IK和FK的原理可以看这个：CSDN

4-1 逆向运动学引言_哔哩哔哩_bilibili

奇异性 (Singularity)

奇异性是指机械臂处于某种特定构型（Configuration）时，其运动学性质发生退化的现象。
数学定义：雅可比矩阵秩亏 (Rank Deficiency)

在微分运动学中，末端速度 $\dot{x}$ 与关节速度 $\dot{q}$ 的关系由雅可比矩阵描述：

\dot{x} = J (q) \dot{q}

当求解逆运动学速度（已知末端速度求关节速度）时，我们需要 $J$ 的逆：

\dot{q} = J^{- 1} (q) \dot{x}

奇异位形即指使得雅可比矩阵 $J (q)$ 行列式为零（ $det (J) = 0$ ）或秩（Rank）减少的构型。此时， $J$ 不可逆（或是奇异矩阵）。

物理/工程表现

自由度丧失：在奇异点，机械臂在笛卡尔空间的某个特定方向上完全失去移动能力。无论关节如何运动，末端都无法沿该方向产生瞬时速度。
无限关节速度：根据 $\dot{q} = J^{- 1} \dot{x}$ ，当 $J$ 趋近于奇异（行列式趋近于0）时，为了维持一个有限的末端笛卡尔速度 $\dot{x}$ ，计算出的关节速度 $\dot{q}$ 会趋向于无穷大。
- 后果：导致控制系统输出饱和、电机过载、机械臂剧烈震动甚至失控。

分类

边界奇异性 (Boundary Singularity)：发生在工作空间边缘（机械臂完全伸直或折叠）。此时机械臂无法进一步向外延伸。
内部奇异性 (Internal Singularity)：发生在工作空间内部。通常是由于两个或多个关节轴线共线（Collinear）或对齐造成的。例如，6轴机械臂的腕部关节轴线重合（Wrist Singularity），导致无法唯一确定末端姿态

冗余度 (Redundancy)

冗余度是指机械臂拥有的自由度（DOF）数量多于执行特定任务所需的最少自由度数量。

数学定义：维数差异 ( $n > m$ )

设关节空间的维数为 $n$ （关节数），任务空间（笛卡尔空间）的维数为 $m$ （通常为位置3 + 姿态3 = 6）。

当 $n > m$ 时，称该机器人为冗余机器人（Redundant Robot）。
例如：一个 7自由度（7-DOF）的机械臂去执行一个 6自由度（6-DOF）的抓取任务，它就拥有 1 度的运动学冗余。

核心特性：零空间运动 (Null Space Motion)

对于冗余机器人，逆运动学问题从“求唯一解”变成了“求无限多解”。

数学上，这对应于雅可比矩阵拥有非空的零空间（Null Space）。

我们可以将关节速度分解为两部分：

\dot{q} = J^{†} \dot{x} + (I - J^{†} J) {\dot{q}}_{0}

第一项 $J^{†} \dot{x}$ ：完成特定任务所需的最小范数解（其中 $J^{†}$ 是伪逆矩阵）。
第二项 $(I - J^{†} J) {\dot{q}}_{0}$ ：零空间投影项。

物理意义：这就意味着存在一种运动，即机械臂的关节在动，但末端执行器保持完全静止（这种运动被称为“自运动”或 Self-motion）。

一句话解释：机器人的关节比任务需要的多，所以它干活时特别灵活，可以“花式”干活。

通俗比喻：你的手肘

做一个实验：

把你的右手掌按在桌面上，按死不动（这代表任务：保持末端位置不变）。
现在，试着摇晃你的手肘。
你会发现，虽然手掌没动，但你的手肘可以向上抬、向外拐、甚至画圈。

这就是冗余度。因为你的任务只是“按住桌子”（只需要 6 个自由度），但你的人体手臂系统其实很复杂（超过 6 个自由度），多出来的自由度就让你可以在不耽误干活的前提下，随意调整胳膊的姿势。

概念	为什么产生 (Why)	什么时候出现 (When)	形象理解
冗余度	资源过剩。机器人的本事(自由度)比任务要求的更多。	1. 使用 7轴机器人时。 2. 任务有对称性（如激光）忽略某个方向时。 3. 车载机械臂联动时。	手按在桌上不动，胳膊肘还能随便晃。
奇异性	几何重合。关节轴线对齐，导致多个关节功能重复，少了一个控制维度。	1. 腕部关节伸直 ( $J_{5} = 0$ )。 2. 手臂完全伸直到极限。 3. 手伸到了头顶正上方。	两个轮子的车，轮子都横过来了，你非要让它直着走。

3.3 问题：

3.3.1 正运动学和逆运动学的输入和输出是什么？

正运动学 (Forward Kinematics):

- 已知所有关节的角度 $(J_{1} \dots J_{6})$ $\to$ 算出末端在空间的坐标 $(X, Y, Z)$ 。

- 这是为了让系统知道“我现在在哪”。

逆运动学 (Inverse Kinematics):

- 已知想要去的空间坐标 $(X, Y, Z)$ $\to$ 反推出每个关节应该转多少度 $(J_{1} \dots J_{6})$ 。

- 这是为了执行命令，例如“去抓那个工件”。

3.3.2 一个平面两关节机械臂去到同一个目标点，可能会有几种解？为什么？

通常有 2 种解（但在特殊位置只有 1 种或无数种）。

为什么通常是 2 种？（多解性）

这可以用 “手肘朝向” 来直观理解。

想象你的手臂平放在桌面上（平面二连杆）：

你的肩膀是基座（Base）。
你的指尖按在桌上的一个点（目标点）。
保持指尖和肩膀不动，你的手肘可以往左凸出去，也可以往右凸出去。

这两个姿态：

肘部向上/左 (Elbow Up/Left)
肘部向下/右 (Elbow Down/Right)

尽管关节角度 $(θ_{1}, θ_{2})$ 完全不同，但末端都到达了同一个坐标 $(x, y)$ 。在数学上，这是因为两个圆（以基座为圆心半径 $L_{1}$ 的圆，和以目标点为圆心半径 $L_{2}$ 的圆）通常有两个交点。

1. 特殊情况（奇异点 Singularity）

1 种解： 当目标点处于最远边界（手臂完全伸直， $L_{1} + L_{2}$ ）或最近边界（手臂完全折叠， $| L_{1} - L_{2} |$ ）时。此时两个解重合了。
无数种解： 如果 $L_{1} = L_{2}$ 且目标点刚好在基座原点 $(0, 0)$ 。此时第一关节转到任何角度，第二关节只要折叠回来都能回到原点。

3.3.3 如果目标点超出了机械臂的最大工作范围，会怎样？

机械臂逆运动学求解不出到达目标点的姿态，卡死，进入危险区域，可能会导致电机烧毁

4 高阶数学工具：旋量代数

4.1 目标：

理解现代机器人学中的数学工具（李群、李代数）。

4.2 内容：

4.2.1 Twist（螺旋向量）的定义

4.2.2 旋量表示：位姿 = Exponential of a Twist

4.2.3 指数映射与对数映射

4.2.4 应用：利用旋量计算刚体运动、轨迹

4.3 问题：

4.3.1 什么是“斜对称矩阵”？

4.3.2 Twist（螺旋向量）由哪两部分组成？

4.3.3 “刚体位姿等于一个螺旋的指数映射”是什么意思？

5 附录：运动学正逆解应用

02_邢鉴明_2021212307_ZX_LW_00.jpg