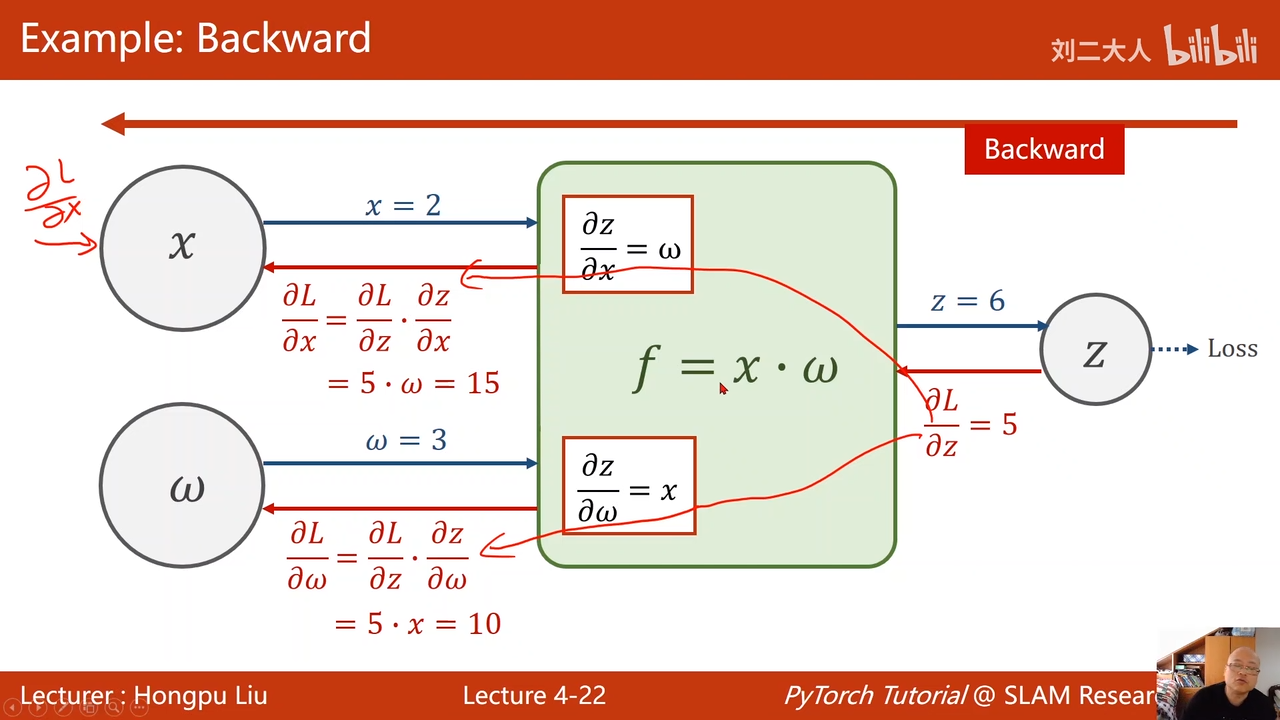
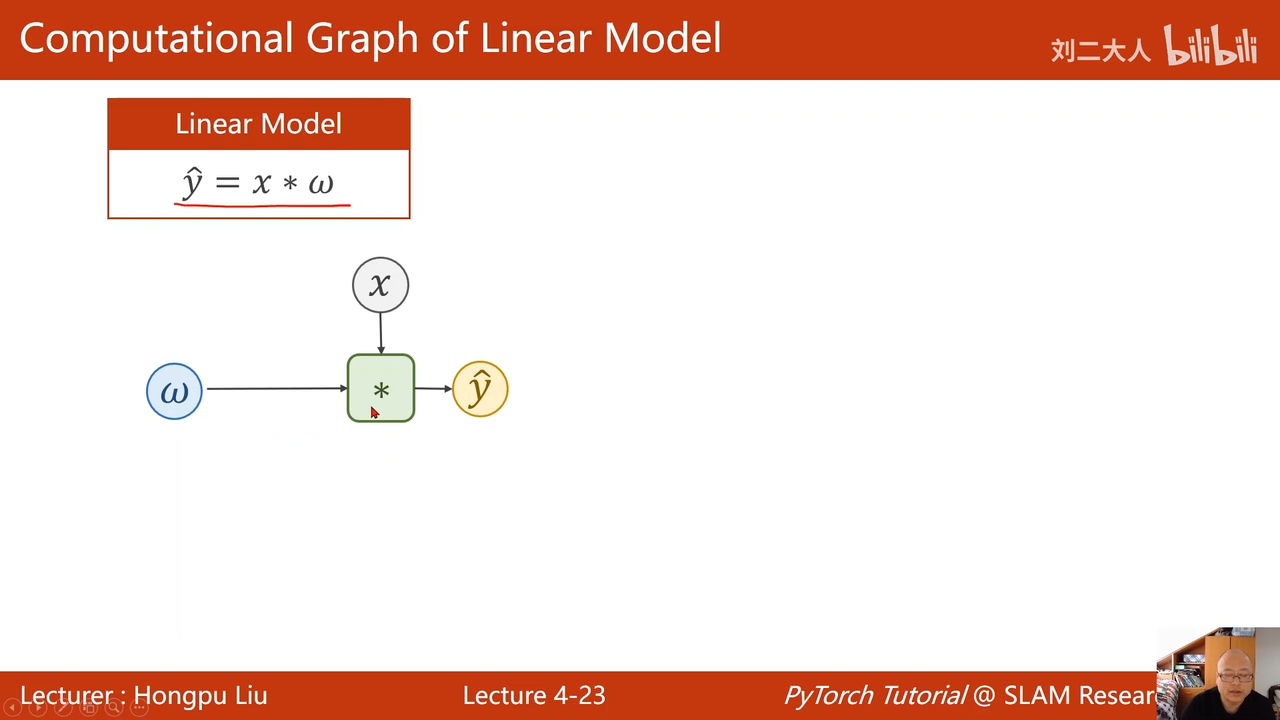
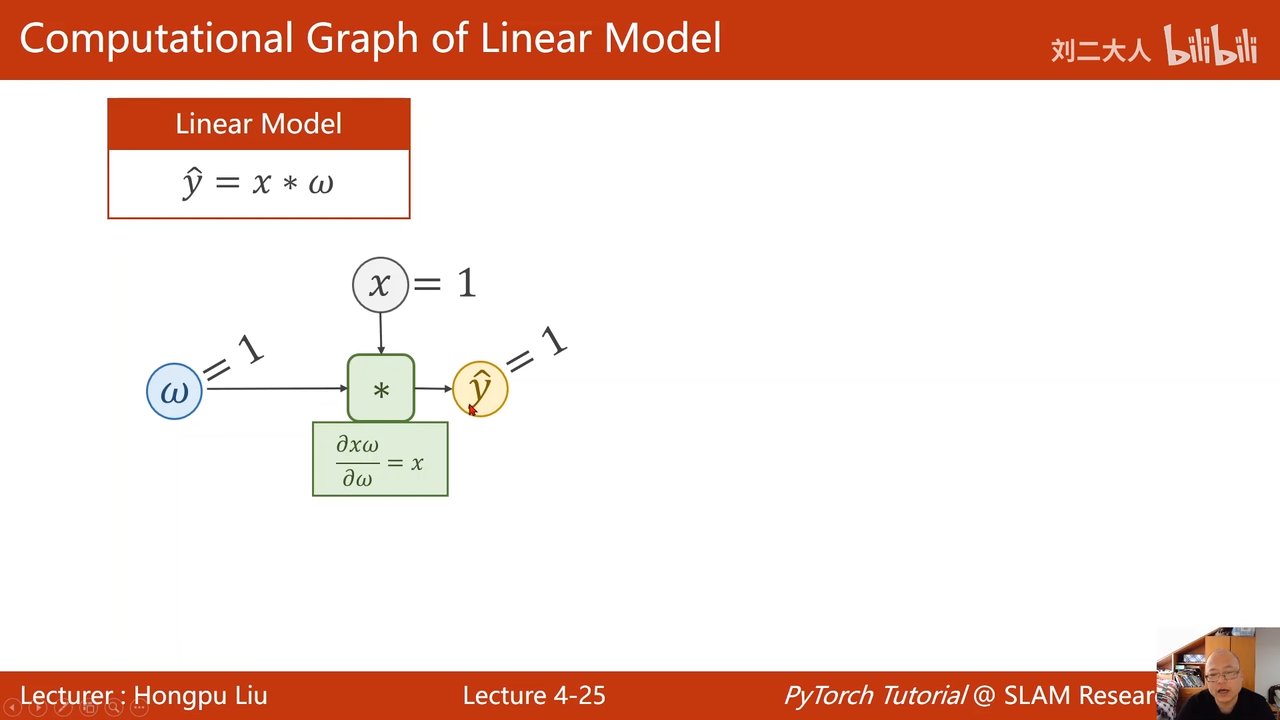
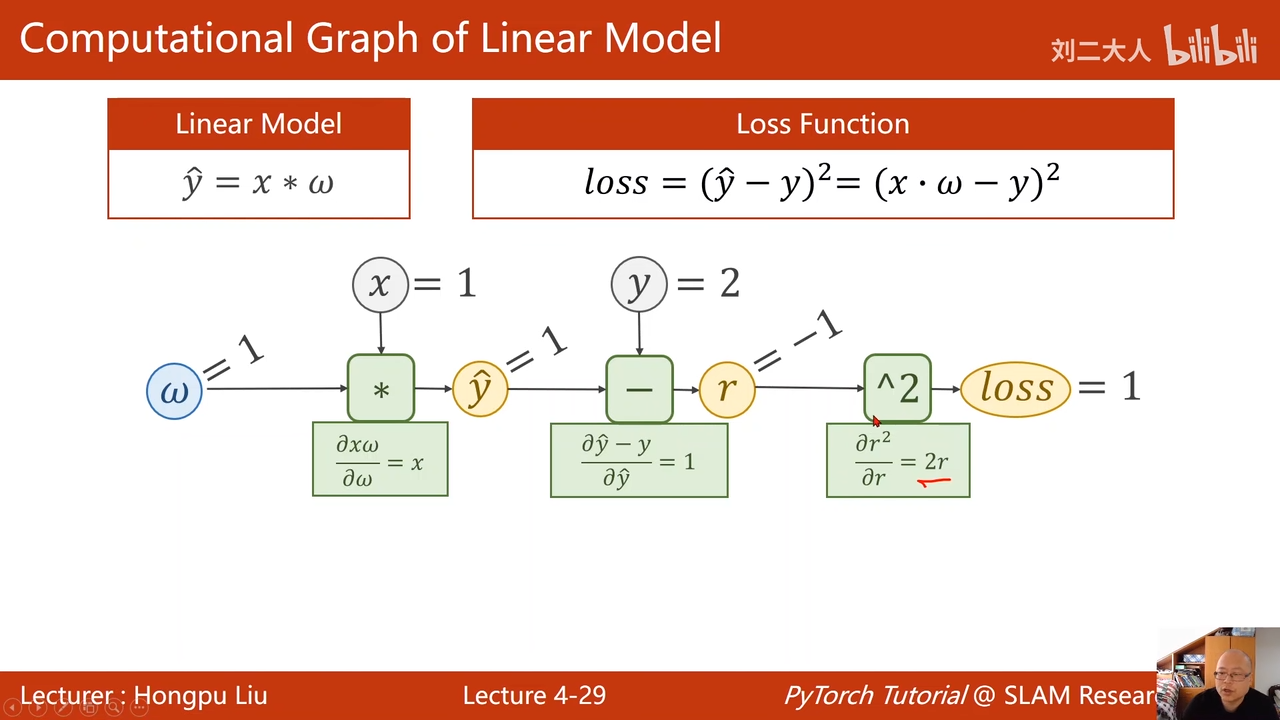
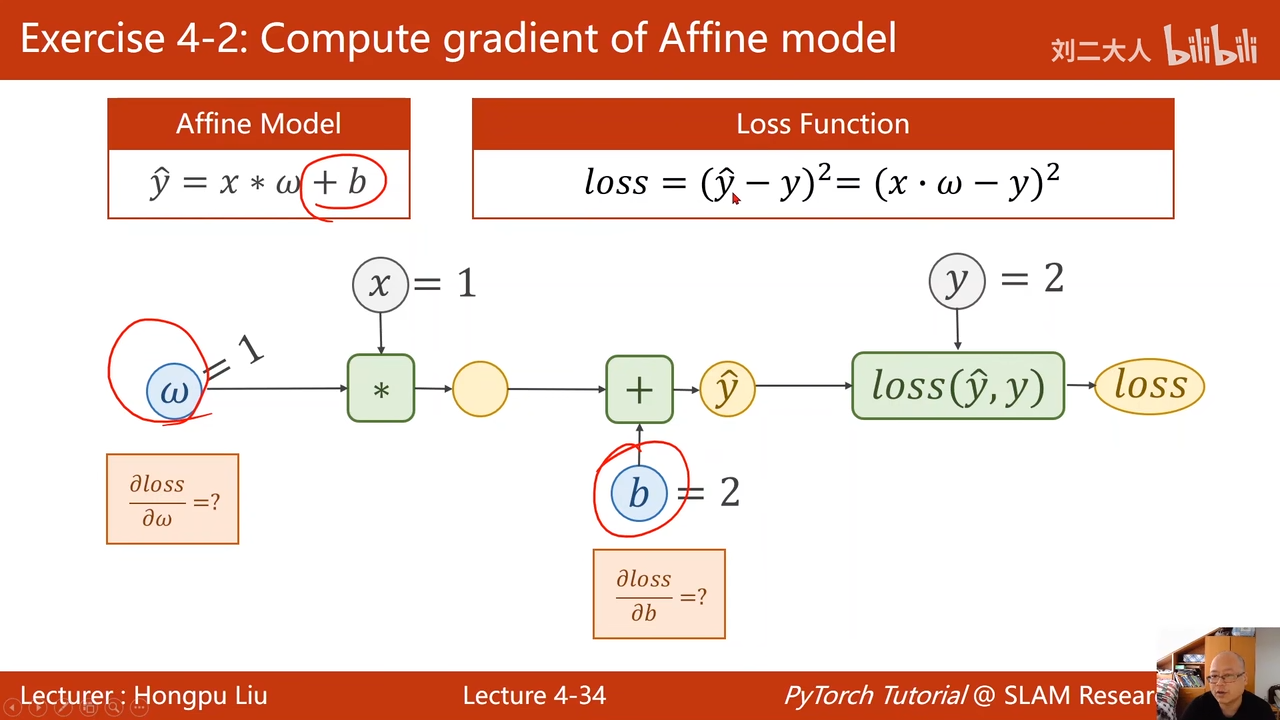
4back propagation(反向传播)
00:02:18.624
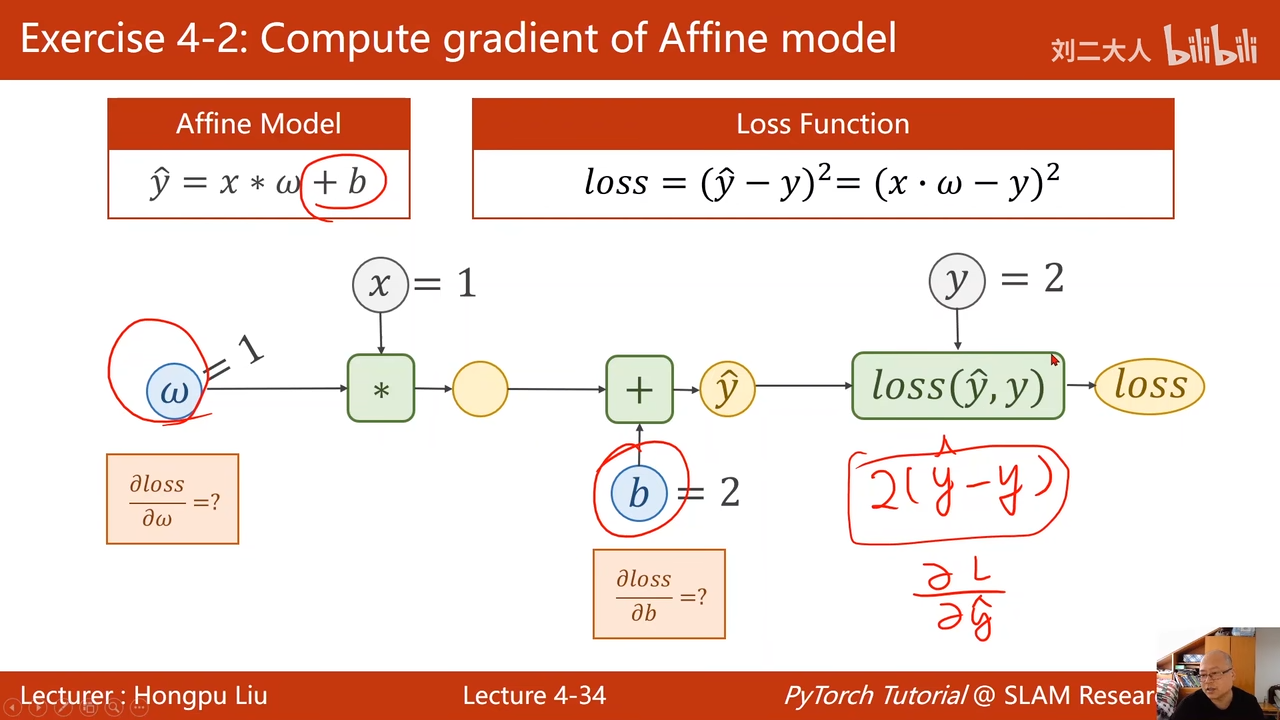
注意这里时对损失进行求导,而不是对
00:02:33.467

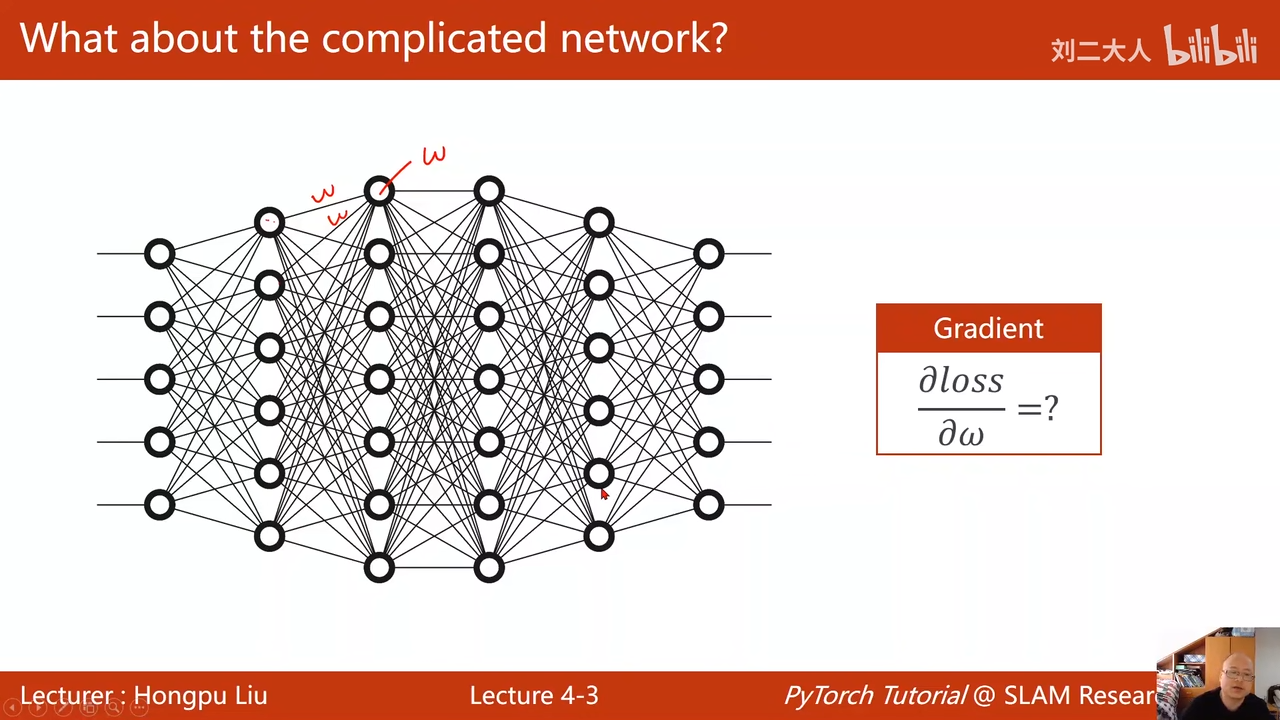
第一层00:03:49.205
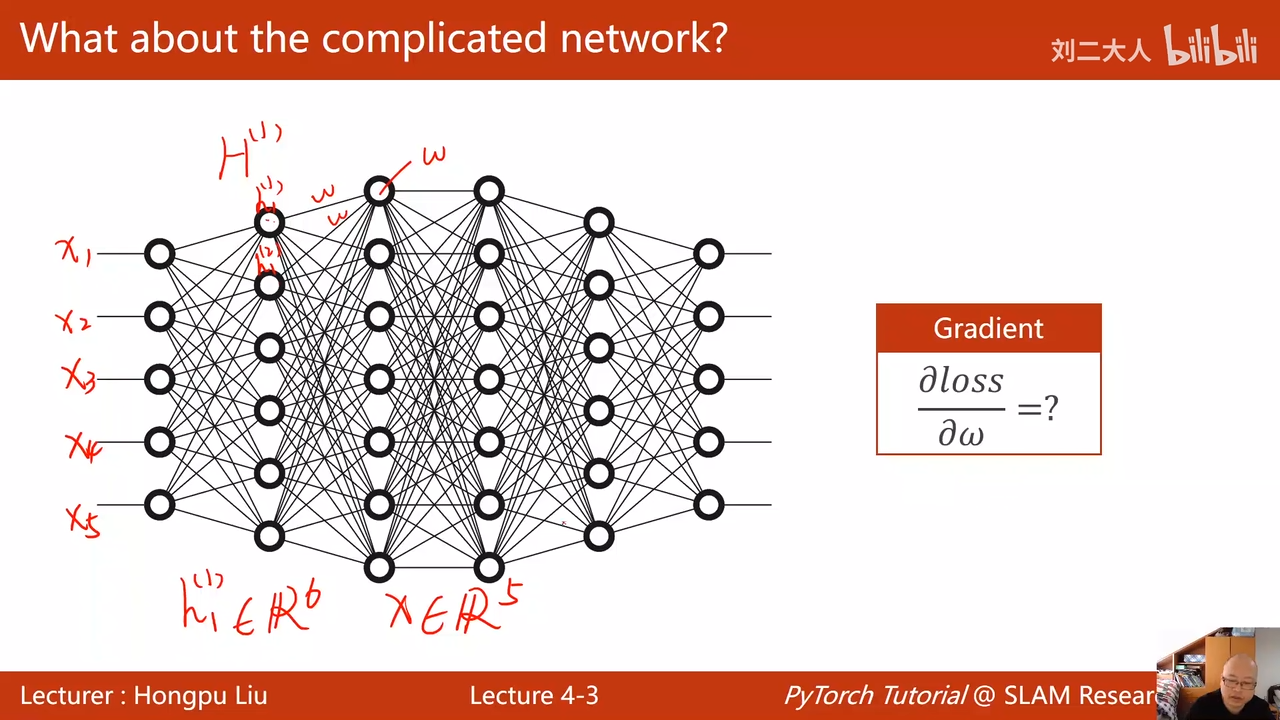
隐层h1第一层,是6维的
x是5维的
隐层h2 7维
写解析式太麻烦了
面对这样的复杂网络
把网络看成图
再图上进行传播梯度
基于链式法则
00:05:33.953
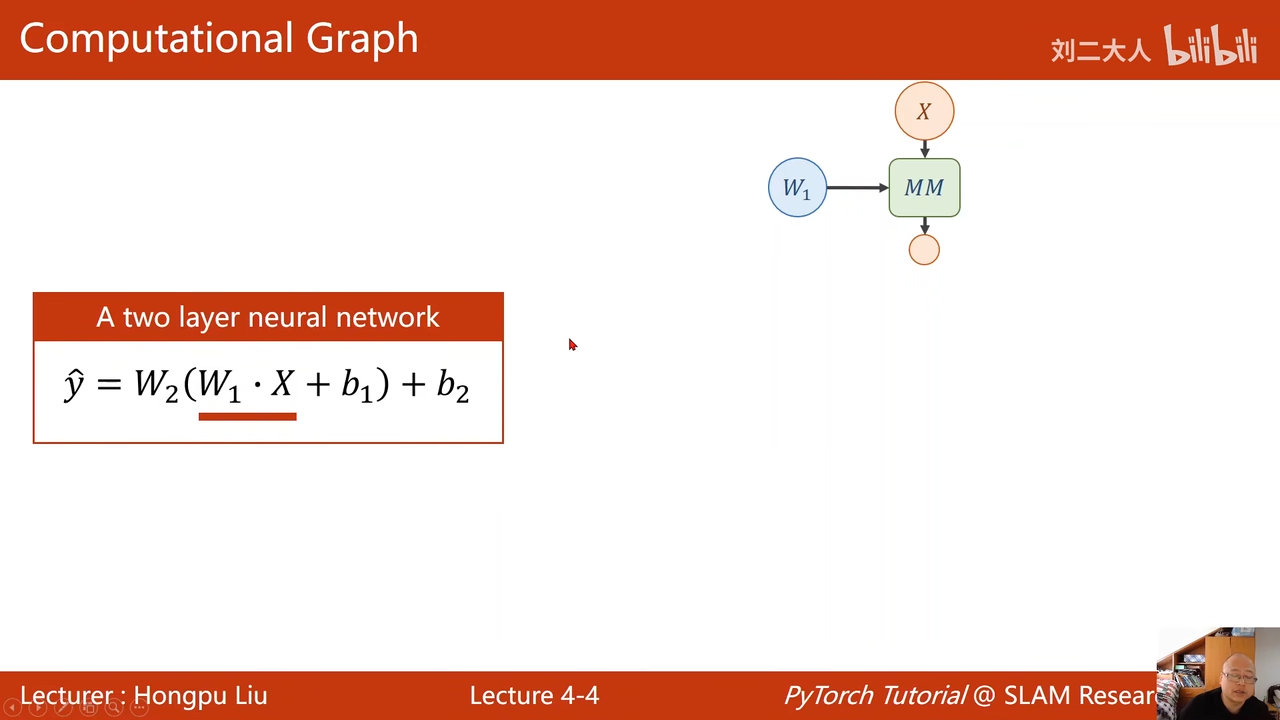
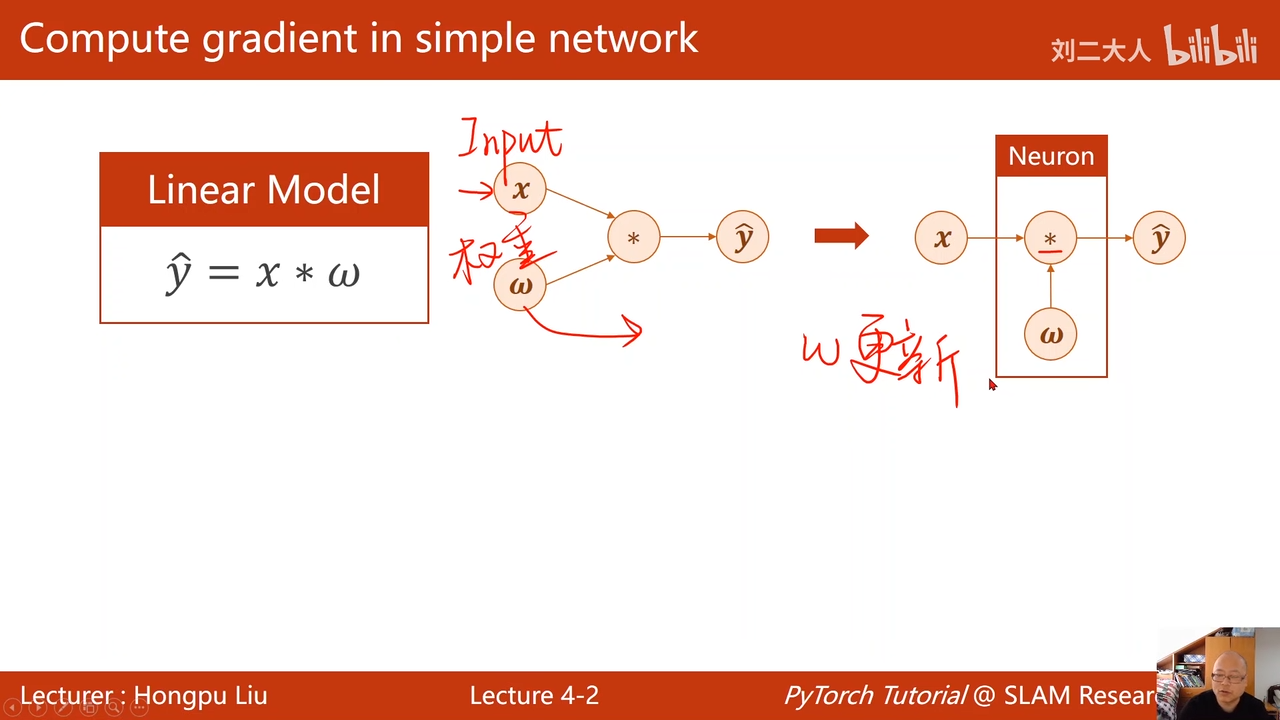
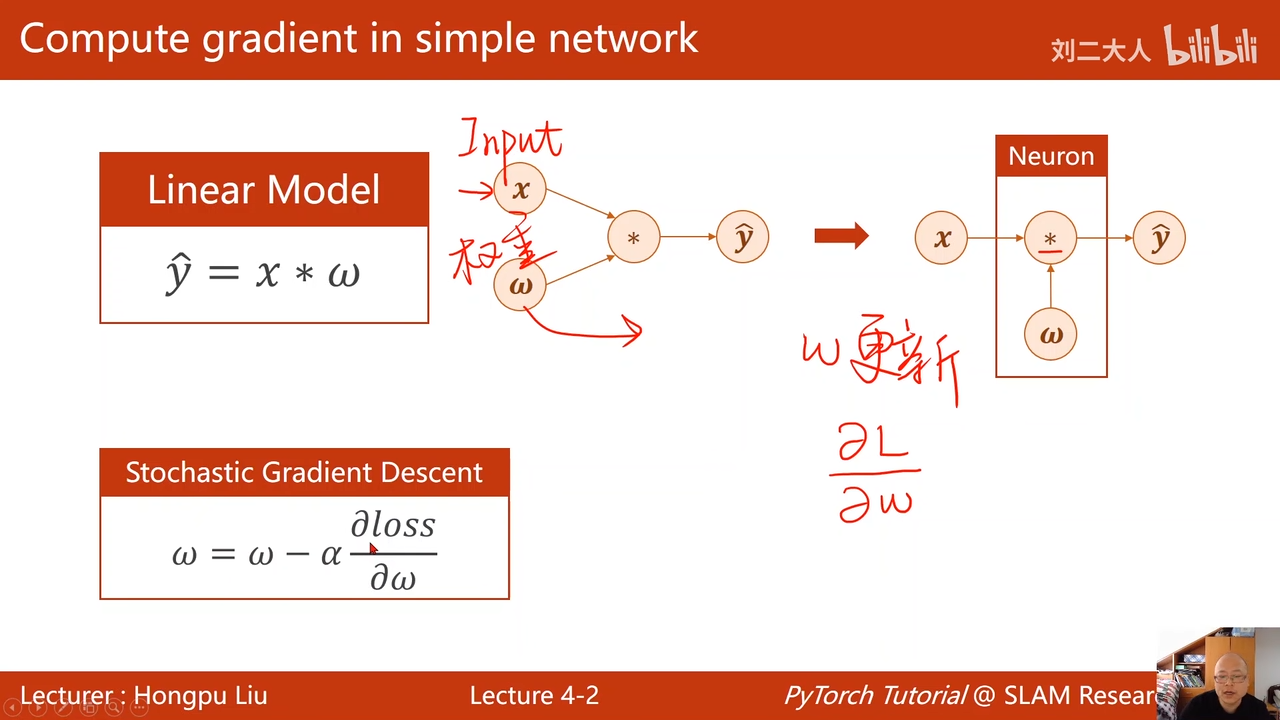
两层神经网络
00:06:52.853

这个转置符号无所谓
x的维数为N
00:07:26.884
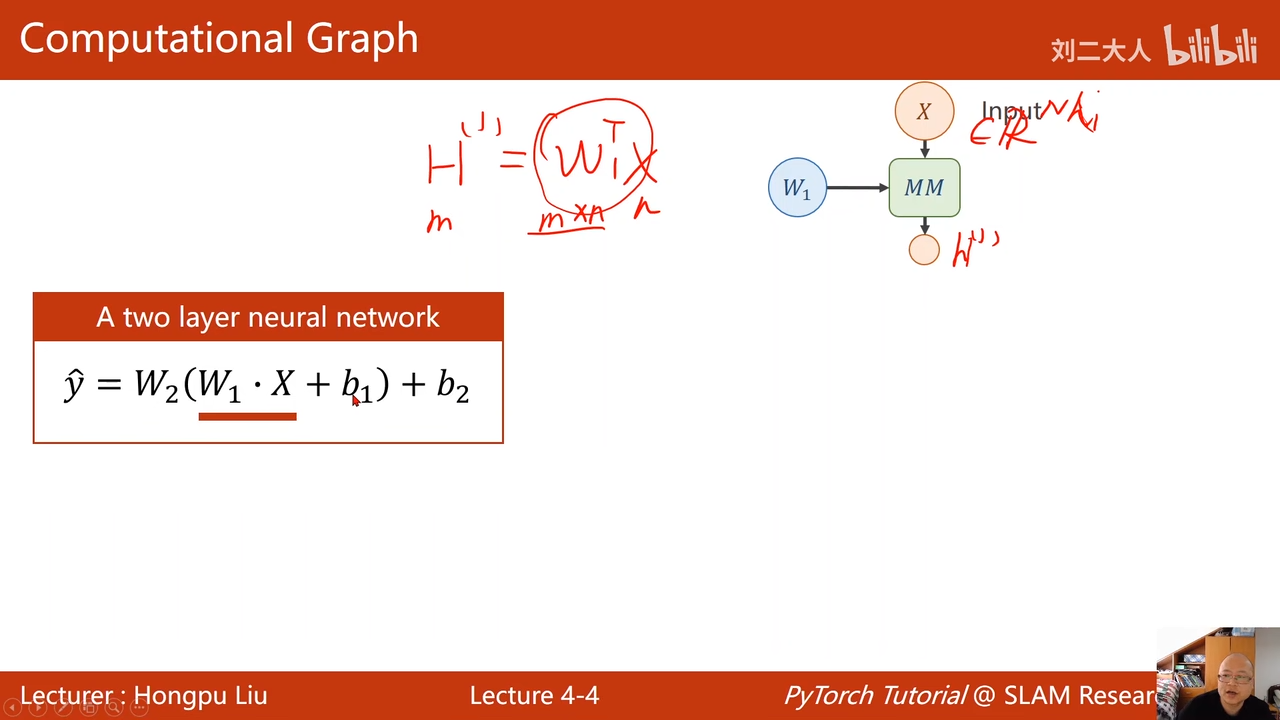
00:08:01.980

h1的维数为m
b1是m维
00:08:58.784

全链接神经网络的第一层
下面是第二层
00:09:52.605

把两层变成1层,不管多少层,线性变换,都可以变成1层。
为了提高模型的复杂程度
00:12:34.502

添加一个非线性的函数,用于提高复杂程度
nonliner
00:13:14.804

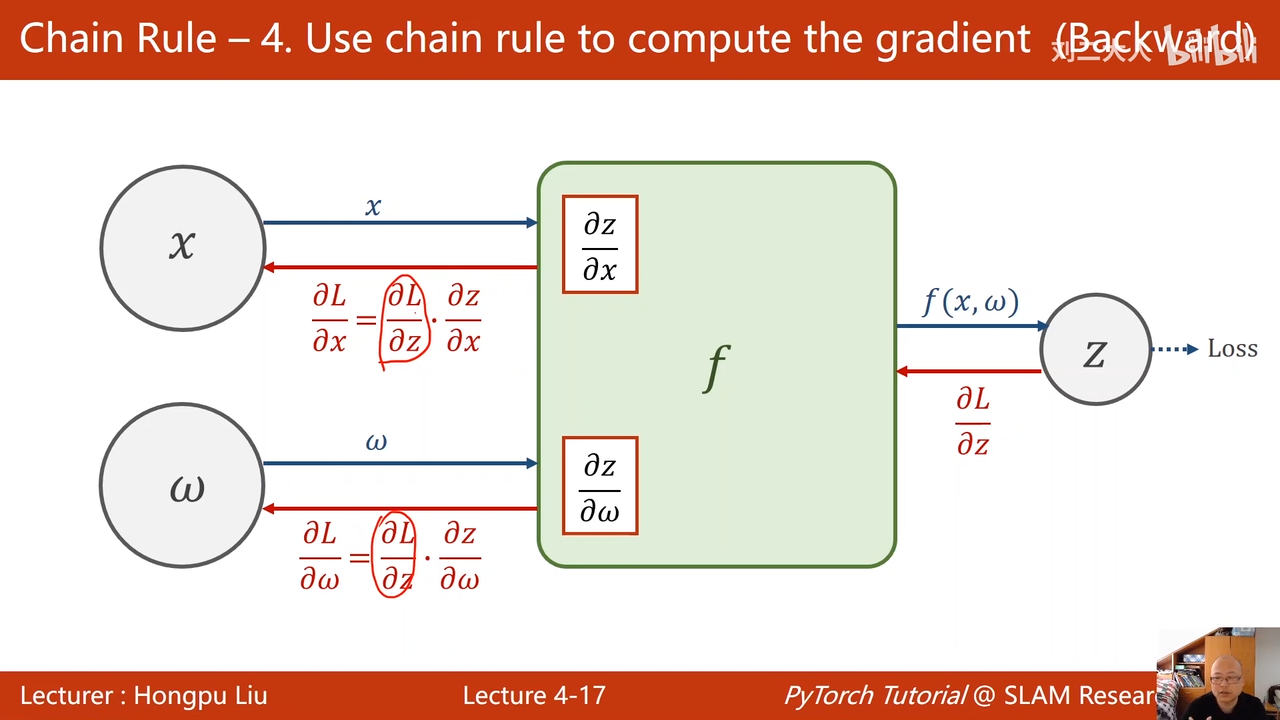
链式求导法则
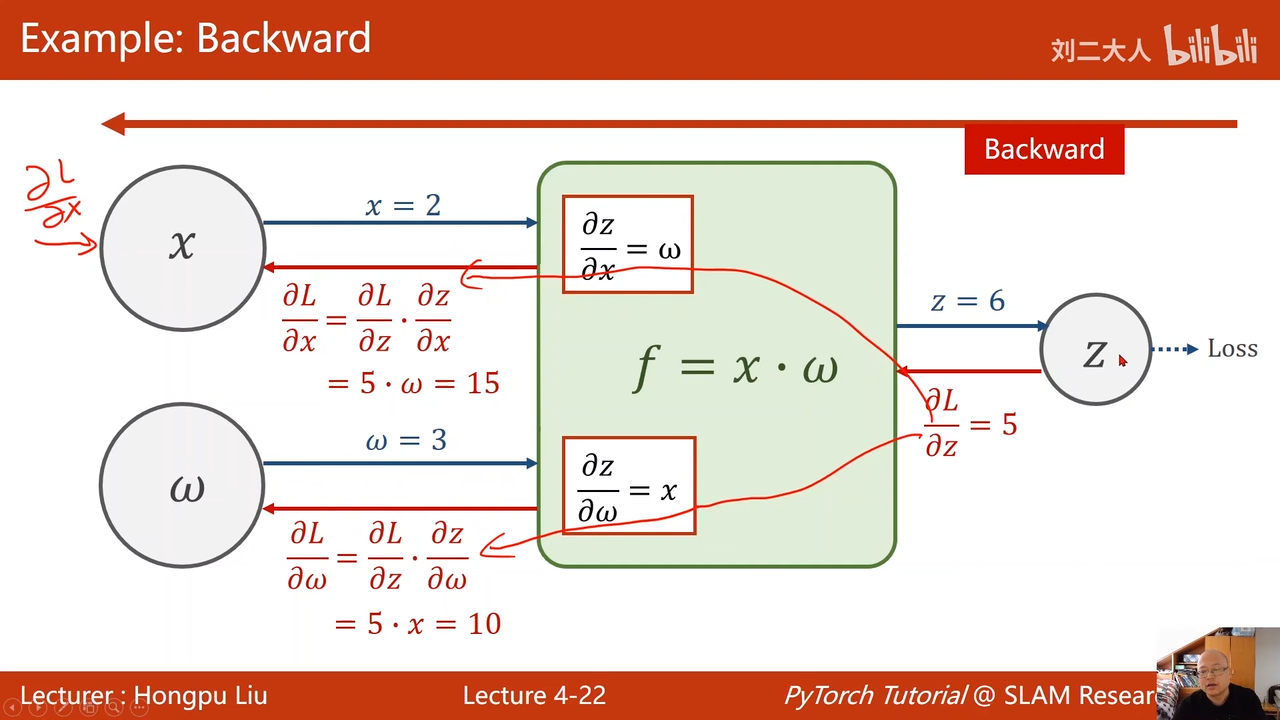
首先进行前馈操作00:16:07.295
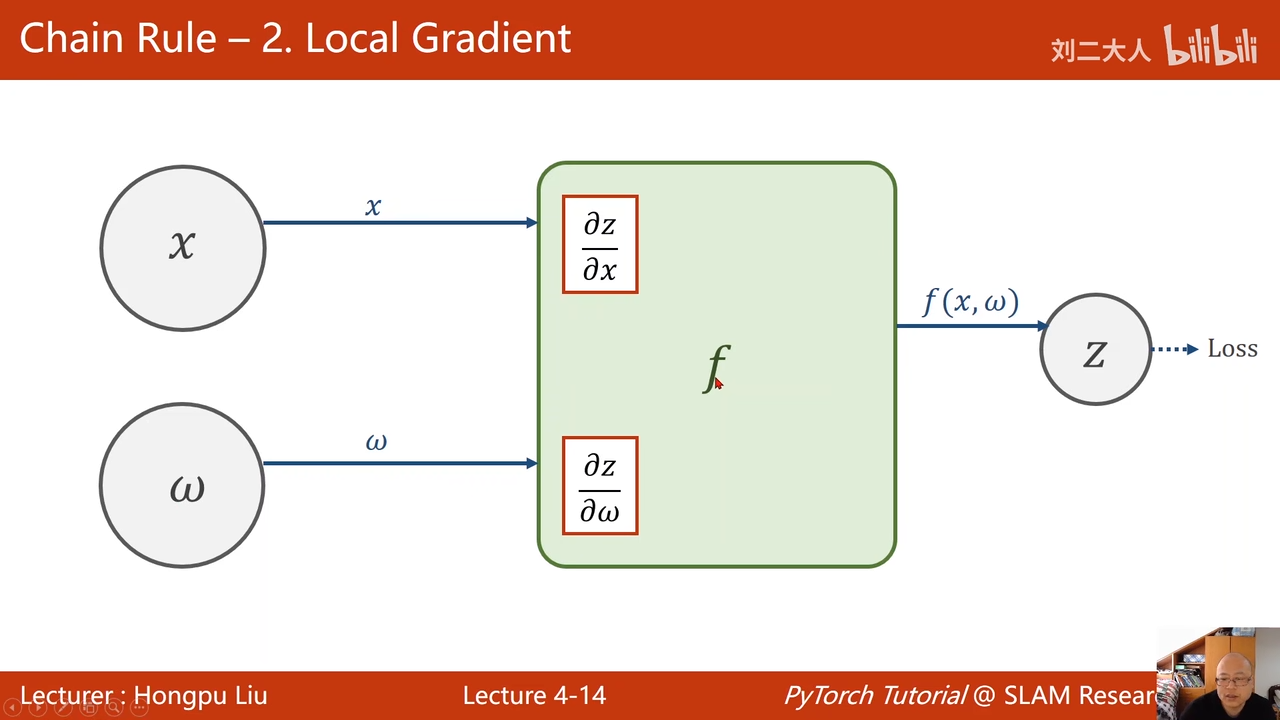
也就是x->z
输出的结果z与实际值要求值之间的差值,对于z求导,这样得到偏导00:17:32.366

在一步一步进行反向传播。
最主要目的还是获得L对w的梯度,实现权重更新
"//"是分数的快捷键
对于 x,其实只有两层神经网络,是用不到的,但是对与超过两层的神经网络来说,就很有必要,因为这里的x会需要继续反向传播回上一层,用于上一层接着计算梯度
{trigger: “par”, replacement: "\frac{ \partial ${0:y} }{ \partial ${1:x} }
然后可可以进行权重更新
在前馈过程中,还计算了梯度
开始进行反向传播
00:24:59.293
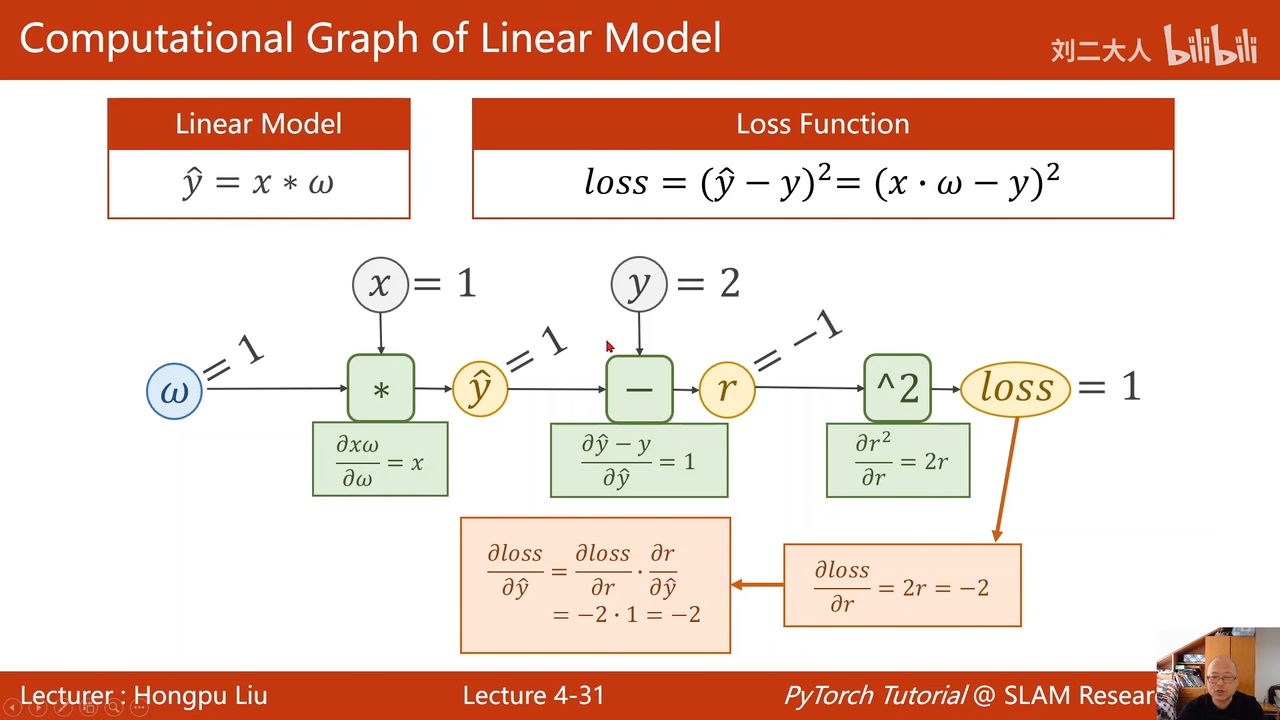
00:26:04.911
image.png

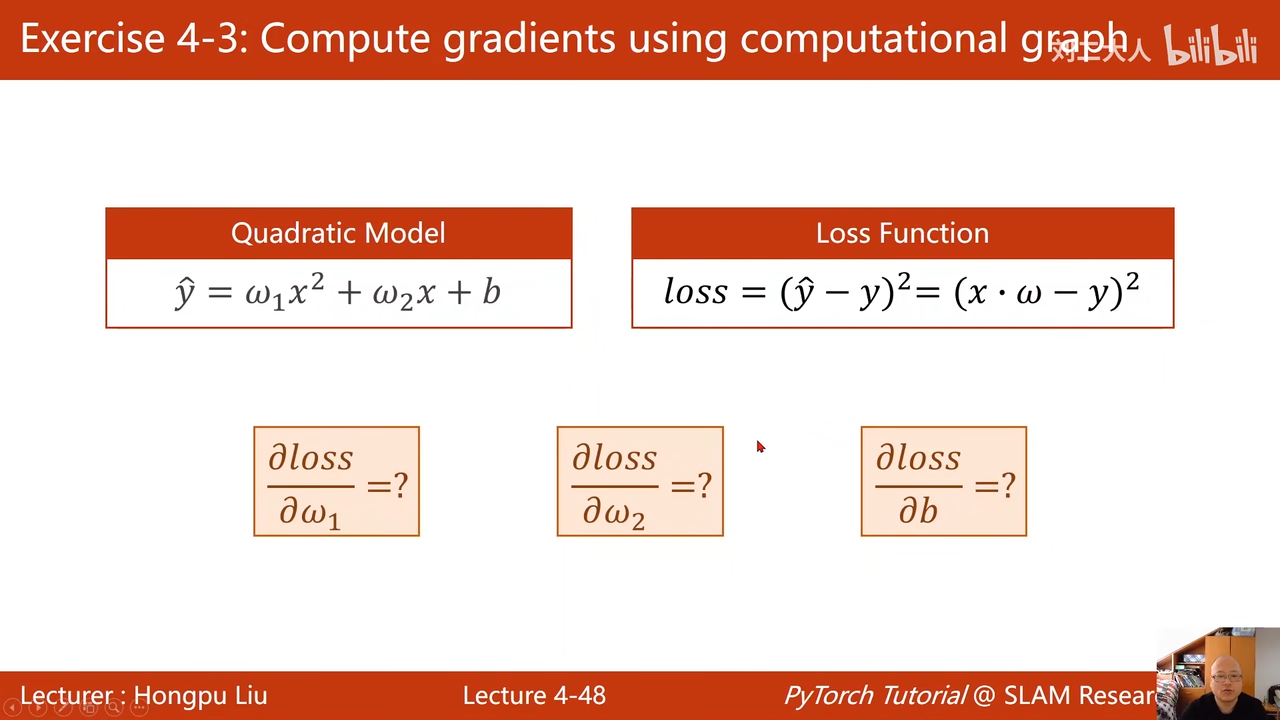
作业:
00:27:26.419

前馈然后反馈
pytorch中进行前馈反馈计算
tensor 保存所有的数值
这个类00:30:35.519

使用pytorch构建神经网络其实就是在构建一个这样的计算图
只有需要计算梯度的时候才设置requires_grad
00:32:28.943

这里w是tensor
所以这里x进行自动的类型转换
因为w需要梯度计算
所以计算结果也需要梯度计算
每调用loss函数就是在构建计算图
训练过程:
00:35:41.707

直接调用backward
就可以进行反向传播
把这个这个计算链路中所有需要梯度计算的值都求出来
00:36:19.110

然后自动把梯度放到变量中
w对应的梯度直接放到w这个类的生成的对象中
调用一次backward之后loss生成的计算图就使用完了,就被释放掉了

下一个epoc进行loss计算就会重新创建一个新的计算图

必须要取到data,因为grad也是一个tensor对象
如果不写,就是在建立计算图
grad.item 用于输出一个标量,来输出梯度
使用sum来计算所有的损失00:41:17.290

因为tensor对象在加法运算中会构建计算图
所以在for循环中重复加法会导致这个计算图特别的长,导致内存爆掉
00:42:08.001

w中数据梯度清零
00:42:46.441

因为w是一个全局变量
而不清零会导致下一轮中加上上一轮的梯度
流程图
00:45:12.777

注意这里需要使用data。而不是直接使用tensor对象来进行更新,因为tensor对象会导致计算图的构建
作业:
00:45:38.919