3梯度下降算法的实现
使用随机猜测
寻找
00:03:10.941

两个权重

这个搜索量太大了
穷举法搜不过来
搜索区间过大导致问题
==分治思想==
00:05:02.292

对于两个权重,进行划分,只考虑这点00:06:02.911

使用这几个点代表所有的空间
分治思想的缺点,会有如上的情况,导致无法获取最低点。有可能会错过比较好的低点
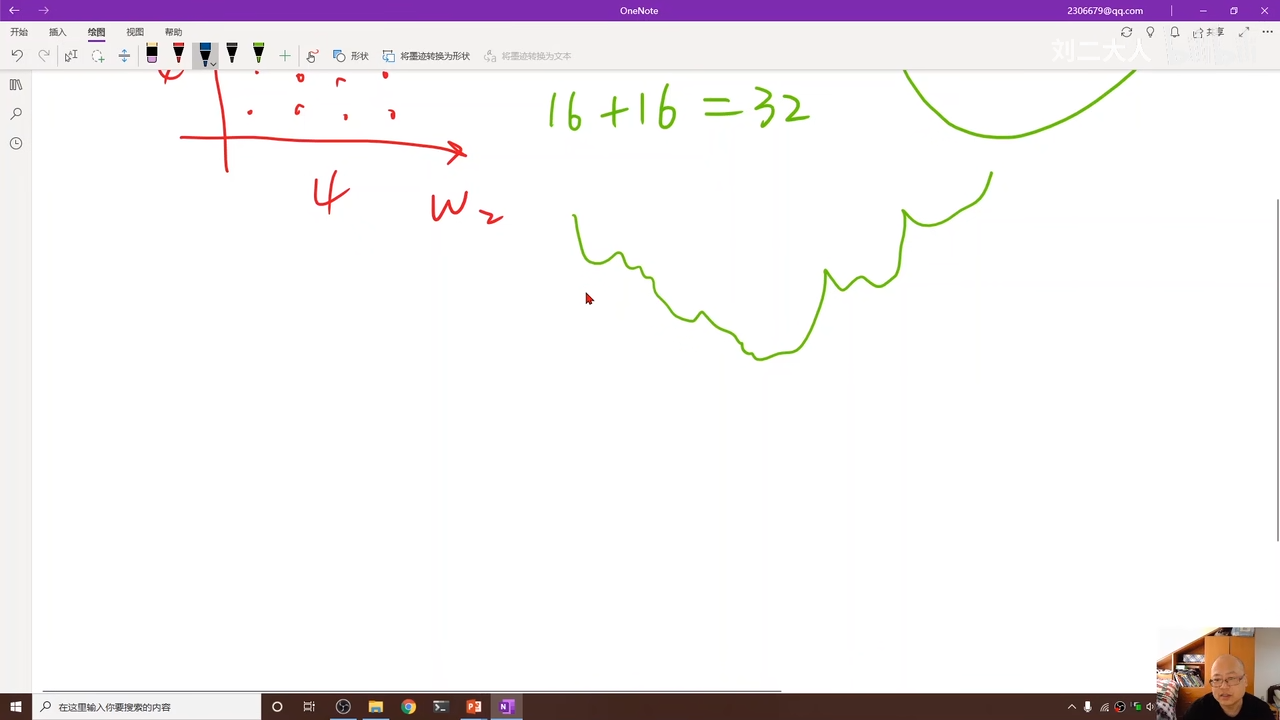
要求函数的最小值
00:11:34.211利用梯度来判断这个点需要进行的平移方向,也就
是如果梯度导数

所以应该选择导数的负方向(下面公式中是负号),用以趋近最低点
00:12:34.364

学习率最好选的小一点
上面的算法思想:
==贪心==

这个被称为非凸函数
就是有一些局部最优点
其实也就极小点
很容易陷入局部最优点
经验总结实际中很少局部最优点
但是鞍点比较麻烦,00:18:09.680

因为这里的梯度等于0,也就是g=0,导致陷入鞍点,无法继续往下走
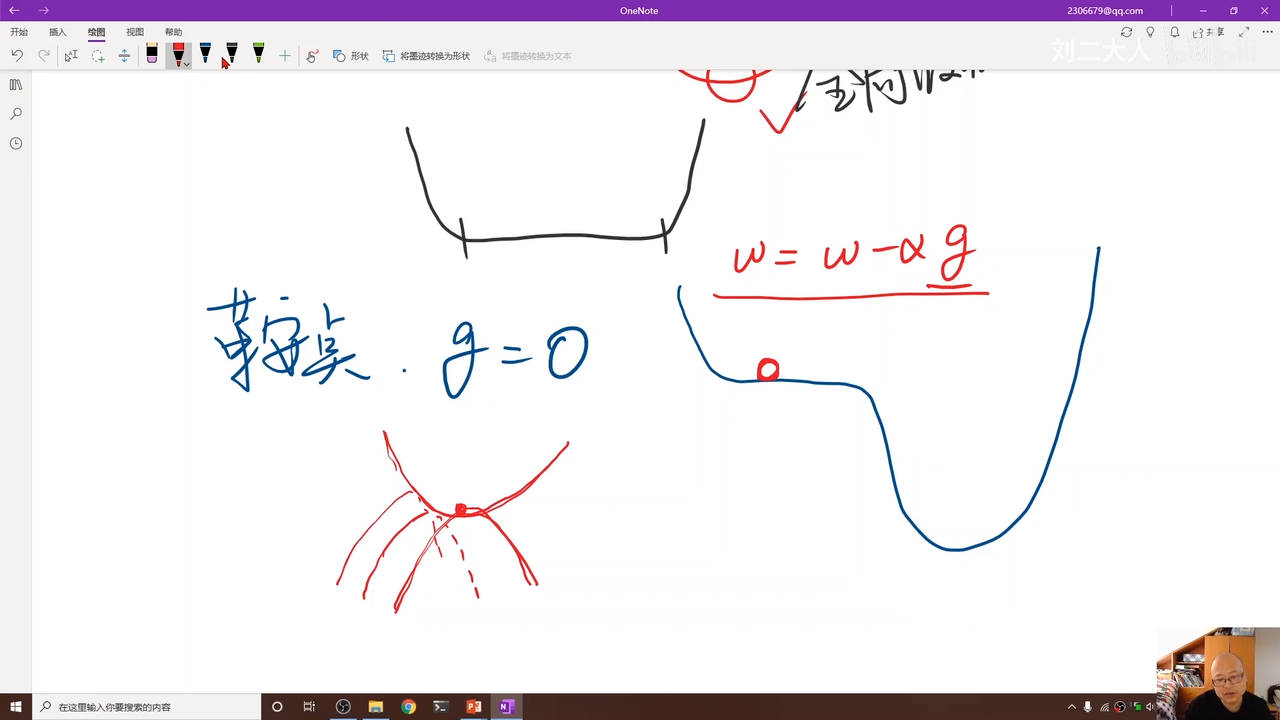
其实就是凹凸函数转变点
比较麻烦
就是二阶导数变化点
对损失函数进行求导
00:22:23.748

更新
猜测初始值
00:23:31.518

前馈
损失函数
这里的xs 和 ys 感觉有点突兀 nnd我是zz,这里是局部变量。
这里表示训练集
00:24:41.133

梯度计算 损失函数求完导数的形式
00:25:21.186

训练过程
00:26:33.213

注意这里的学习率
00:27:05.232

训练结果
随着训练过程 cost越来越低
00:27:48.557

w是权重,权重更新,w是全局变量
最后的这个 4 8
表示当输入量为4时,输出量为8,也就是乘上了w
在收敛之后w固定在了2
00:28:11.612

前面记录损失的下降速度非常快
00:29:12.852
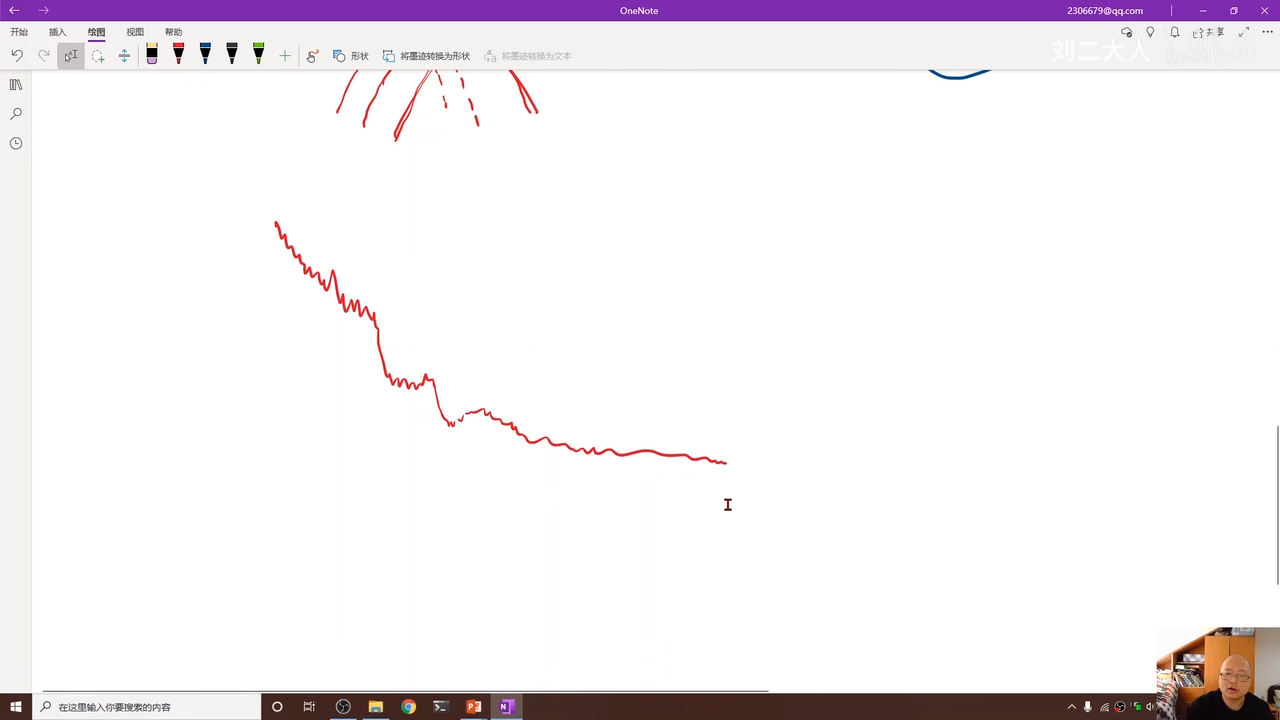
上面是实际的波动过程
总体上时收敛的就可以接受
实际中的图像上面一样不平滑所以画图的时候可以进行 指数加权均值 用来平滑曲线
公式就是修改cost
00:30:40.479

公式如有上图右下
00:30:48.855

00:30:57.135
错误典范,最后发散了,这个横坐标时epoc
常见错误时学习率太大了
梯度下降不常用
最常用的还是随机梯度下降
gradient 使用的整个损失,也就是平均损失,作为依据
而随机梯度下降则是,N个样本中的随机挑选的一个的损失函数
单个样本损失对权重求导
使用原因
为了解决鞍点问题
所有的点都是有噪声的
00:34:09.693

引入一个随机噪声,可能会把我们向前推进
这个被实践证明有效
这里的损失函数计算不再计算平均值
00:35:13.138

这里的梯度不再除以样本量
所有使用的样本都会导致权重的更新
对于每一个样本进行权重更新
00:37:15.354

梯度下降可以使用并行算法,算的快
这里可以理解为,由于没有了均值计算,每一次的权重更新都会导致后续权重更新受到影响,所以
随机梯度下降不可以并行
00:37:46.642

| 算法 | 时间复杂度 | 训练结果好坏 |
|---|---|---|
| 随机梯度算法 | 高 | 好 |
| 梯度算法 | 低 | 坏 |
| 批量的随机梯度下降 | ||
| 00:40:05.899 | ||
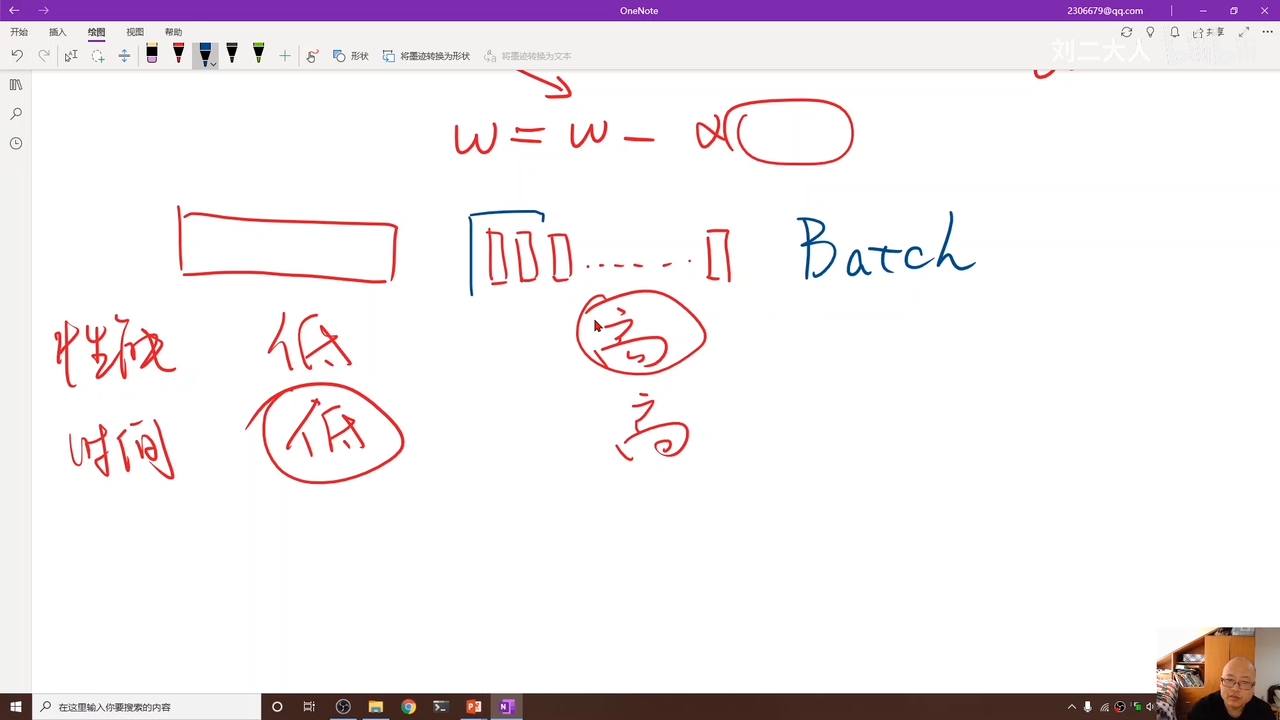 |
mini-batsh=batch
batch解释:
使用数据集中的小批量的随机梯度下降
00:41:06.314